Experimentelles und fortschrittliches Webdesign sucht immer wieder nach neuen Möglichkeiten, mit allen verfügbaren technischen Mitteln die User Experience umfassend zu gestalten. Angesichts der weiterhin wachsenden Bedeutung einer auf alle erdenklichen Endgeräte abgestimmten Webseite wird die kreative Einbeziehung des User-Inputs in Form der Geräteausrichtung immer beliebter – nicht nur für Virtual- und Augmented-Reality-Anwendungen. In den meisten Smartphones sind mittlerweile Gyroskop, Akzelerometer und Kompass verbaut, um die Position, Drehung, Beschleunigung und geographische Ausrichtung des Geräts im Raum bestimmen zu können.
Mit der seit einigen Jahren verfügbaren DeviceOrientation-API können diese Daten auch für die Webentwicklung genutzt werden. Der Browser-Support ist derzeit einigermaßen gut, aber noch von einigen Alleingängen einzelner Hersteller geprägt. Interessante Effekte können damit aber allemal erreicht werden. Im Folgenden sollen zwei Anwendungsfälle erprobt werden: ein responsiver Farbverlauf und eine Wasserwaage.
Wie das Gyroskop funktioniert
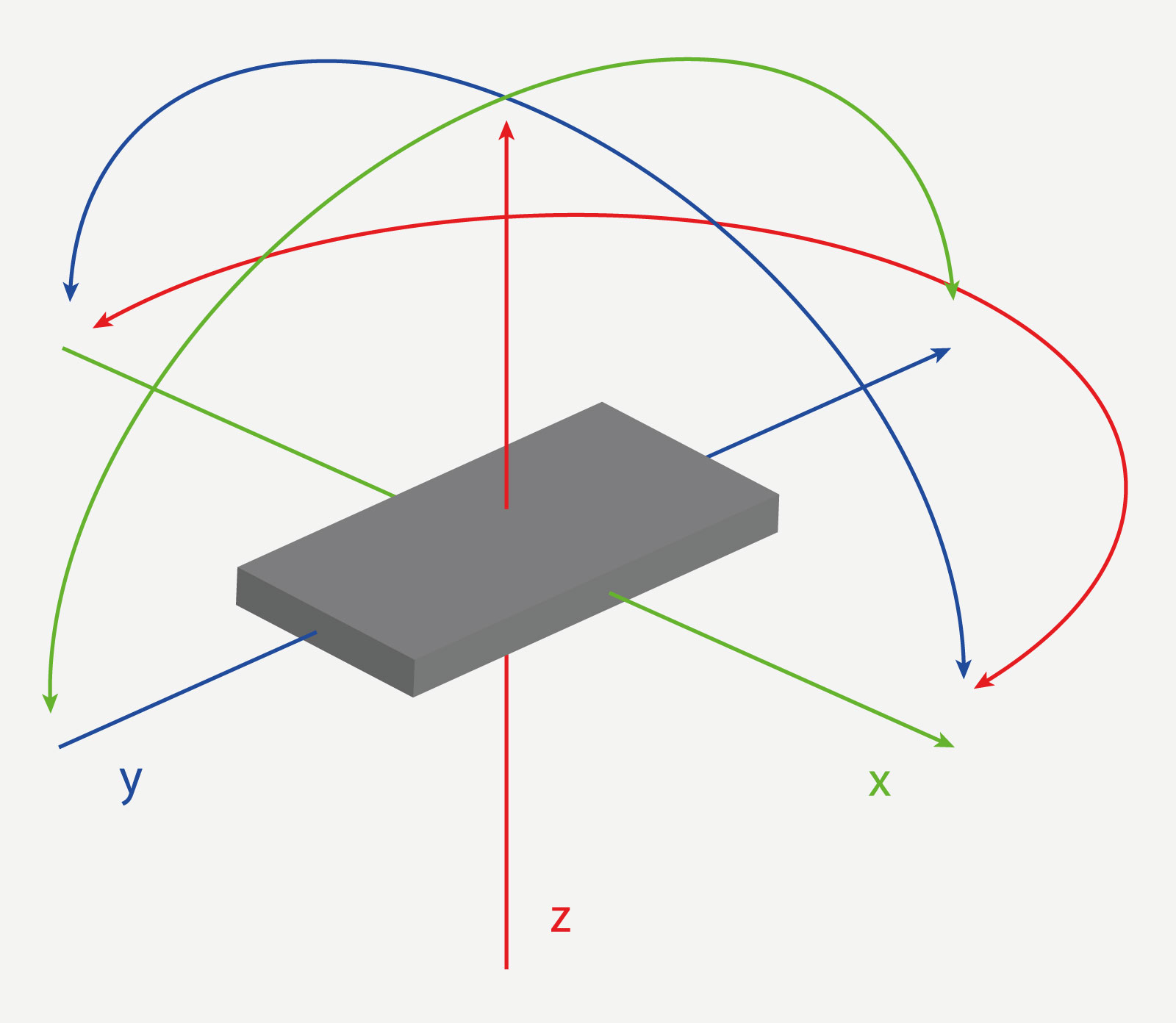
Das Gyroskop kann man sich modellhaft wie einen Kreisel vorstellen, der sich um drei Raumachsen drehen kann. Die x-Achse verläuft von rechts nach links, die y-Achse steht senkrecht dazu in der horizontalen Raumebene und die z-Achse steht senkrecht zu beiden und verläuft von unten nach oben. Diese Achsen sind fest im Raum verankert, sodass die Ausrichtung des Geräts durch drei sog. Eulersche Winkel angegeben werden kann: alpha (die Drehung um die z-Achse), beta (die Drehung um die x-Achse) und gamma (die Drehung um die y-Achse).Dabei ist die Reihenfolge, in denen die Winkel angewandt werden, von Bedeutung. Im Eulerschen Modell werden drei Winkel für zwei Achsen, in der auch in Smartphones genutzten Untergruppe der sog. Tait-Bryan-Winkel dagegen drei Winkel für drei Achsen herangezogen. Dies wird später für die korrekte Berechnung relevant werden.
Dabei kann alpha Werte zwischen 0 und 360, beta zwischen -180 und 180 und gamma zwischen -90 und 90 annehmen. Safari geht hier einen Eigenweg, gibt Werte für beta zwischen -90 und 90 sowie für gamma zwischen -180 und 180 an.
Die Daten auslesen
Zunächst sollte überprüft werden, ob der Browser überhaupt die DeviceOrientation-API unterstützt:
var deviceSupportsOrientation = function() {
return (window.DeviceOrientationEvent || window.DeviceMotionEvent || window.mozOrientation);
}
var currentScreenOrientation = 0;Damit können wir uns entsprechend absichern und in dem Fall, dass der Test false zurückgibt, entsprechend reagieren. Um die Daten der verschiedenen Browser einheitlich wiederzugeben, erstellen wir eine Funktion getDeviceOrientation(), welche bei Änderungen der Geräteausrichtung eine Callback-Funktion cb() ausführt und ein Objekt mit allen Positionsdaten übergibt:
var getDeviceOrientation = function(cb) {
if (!deviceSupportsOrientation()) {
cb(false);
} else {
if ('onorientationchange' in window && typeof(screen.orientation) !== 'undefined') {
window.addEventListener('orientationchange', function() {
currentScreenOrientation = screen.orientation.angle;
}, false);
} else {
window.addEventListener('resize', function() {
currentScreenOrientation = (window.innerWidth / window.innerHeight > 1) ? -90 : 0;
}, false);
}
if (window.DeviceOrientationEvent) {
window.addEventListener("deviceorientation", function () {
cb({ alpha: event.alpha, beta: event.beta, gamma: event.gamma });
}, true);
} else if (window.DeviceMotionEvent) {
window.addEventListener('devicemotion', function () {
cb({ beta: event.acceleration.x, gamma: event.acceleration.y, alpha: event.acceleration.z });
}, true);
} else {
window.addEventListener("mozOrientation", function () {
cb({ beta: orientation.x, gamma: orientation.y, alpha: orientation.z });
}, true);
}
}
}Außerdem fragen wir ab, ob der Browser das onorientationchange-Event unterstützt, das uns hilft, den automatischen Wechsel mancher Smartphones zwischen Hoch- und Querformat zu erkennen. Dazu speichern wir den Wert von screen.orientation.angle in der globalen Variable currentScreenOrientation: 0 im Hochformat, -90 auf rechts und 90 auf links gedreht. Andernfalls bemühen wir das resize-Event, um zumindest zwischen Hoch- und Querformat unterscheiden zu können.
Dadurch können wir uns um die konkrete Verarbeitung in einer eigenen Funktion (etwa reactToPosition()) kümmern, welche wir wie folgt übergeben:
var reactToPosition = function(orientation) {
…
}
window.addEventListener('load', function() {
getDeviceOrientation(reactToPosition);
});Die Daten mit einer Serie von Drehmatrizen korrekt verarbeiten
An dieser Stelle könnte man einfach die Werte für alpha, beta und gamma auslesen und direkt verarbeiten. Wegen der verschiedenen Intervalle, in denen die einzelnen Browser diese Winkel ausgeben, erreicht man damit jedoch keine konsistenten Ergebnisse. Außerdem leidet das Eulersche Winkelsystem am Phänomen des sog. Gimbal Lock, das immer dann eintritt, wenn zwei der drei Rotationsachsen aufeinander fallen, nachdem die erste oder zweite Drehbewegung das System bereits verändert hat. Die Folge ist, dass eine Rotationsachse effektiv verloren geht und das Gesamtsystem in seinem Zustand verharrt oder zwischen gegensätzlichen Winkelpaaren hin- und herspringt. Im Falle des responsiven Farbverlaufs hat das den Effekt eines flackernden Bildes, wohingegen die Wasserwaage plötzliche Sprünge zeigen würde.Eine genauere Beschreibung und eine Animation des Gimbal Lock sind in dem verlinkten Wikipedia-Artikel zu finden.
Beide Probleme können mit einem Zwischenschritt, der Berechnung eines Normalenvektors und einer Drehmatrix, umgehen. reactToPosition() beginnt daher mit:
var reactToPosition = function(orientation) {
var normal = false;
if (orientation !== false && orientation.alpha !== null &&
orientation.beta !== null && orientation.gamma !== null) {
normal = [0, 0, 1];
Zunächst wird überprüft, ob das Objekt orientation nicht false ist (also der Browser über die DeviceOrientation-API verfügt) und ob seine einzelnen Attribute nicht null sind (also ob das Gerät überhaupt gyroskopische Daten misst). Anschließend wird normal als ein Array mit drei Elementen definiert, welche den Koordinaten x, y, und z eines Vektors im dreidimensionalen Raum entsprechen. Vektoren sind, vereinfacht gesprochen, mathematische Objekte in einem Raum, die eine Richtung und eine Länge haben.
Für unsere Zwecke wird normal zunächst als Vektor in Richtung der z-Achse definiert, der eine Länge von 1 hat. Damit ist einer sog. Einheitsvektor und kann durch einfache Multiplikation all seiner Elemente mit einem Faktor beliebig verlängert oder verkürzt werden. normal zeigt also direkt nach oben, also bezogen auf das Gerät aus dem Bildschirm direkt Richtung Himmel.
Ziel ist es, diesen Vektor mit einer Drehmatrix so zu rotieren, dass er die genaue Ausrichtung des Geräts beschreibt (und die Länge 1 behält). Dazu wird eine Matrix definiert und in mehreren Schritten durch verschiedene Funktionen verändert, ehe sie auf den Normalenvektor angewendet wird.
Die Matrixtransformationen
var matrix = getBaseRotationMatrix(orientation.alpha, orientation.beta, orientation.gamma);
matrix = multiplyMatrix(matrix, getScreenMatrix());
normal = multiplyVector(normal, matrix);Zunächst wird eine Drehmatrix definiert, die mithilfe der drei Ausrichtungswinkel des Geräts einen genormten Faktor berechnet, der später auf jeden Vektor (und auch unseren Normalenvektor) angewendet werden kann und diesen dann genau in dieselbe Richtung dreht. Die Funktion getBaseRotationMatrix() ist der Kern unseres Algorithmus, da er sowohl den Gimbal Lock eliminieren als auch die unterschiedlichen Winkelintervalle der einzelnen Browser ausgleichen kann.
var getBaseRotationMatrix = function(alpha, beta, gamma) {
alpha = alpha ? degreeToRad(alpha) : 0;
beta = beta ? degreeToRad(beta) : 0;
gamma = gamma ? degreeToRad(gamma) : 0;
var cA = Math.cos(alpha),
cB = Math.cos(beta),
cG = Math.cos(gamma),
sA = Math.sin(alpha),
sB = Math.sin(beta),
sG = Math.sin(gamma);
var m11 = cA * cG - sA * sB * sG,
m12 = -cB * sA,
m13 = cG * sA * sB + cA * sG,
m21 = cG * sA + cA * sB * sG,
m22 = cA * cB,
m23 = sA * sG - cA * cG * sB,
m31 = - cB * sG,
m32 = sB,
m33 = cB * cG;
return [ m11, m12, m13,
m21, m22, m23,
m31, m32, m32 ];
}Im Wesentlichen berechnet die Funktion eine vereinte Drehmatrix, welche der drei auf einander angewandten Drehmatrizen um die z-Achse, dann um die x- und schließlich um die y-Achse entspricht.Während die Eulerschen Winkel (und damit auch die Tait-Bryan-Winkel) in einer bestimmten Reihenfolge angewendet werden müssen, steht uns dies in einem solchen System aus Rotationsmatrizen frei. Schreibt man die einzelnen Matrixmultiplikationen zwischen den drei Matrizen aus, erhält man die obigen Gleichungen für die Koordinaten m11 bis m33. Da die trigonometrischen Funktionen in JavaScript Winkelangaben in Radians erfordern, werden die drei Winkel anfangs konvertiert:
function degreeToRad(angle) {
return angle * Math.PI / 180;
}Mit getBaseRotationMatrix() haben wir zwar bereits den wesentlichen Teil geschafft, jedoch muss noch der Wechsel zwischen Hoch- und Querformat berücksichtigt werden. Die Funktion getScreenMatrix() gleicht dies aus, indem sie eine weitere Drehmatrix berechnet, welche die Drehung entgegen des Winkels currentScreenOrientation vornimmt.
var getScreenMatrix = function() {
var cosZ = Math.cos(currentScreenOrientation),
sinA = Math.sin(currentScreenOrientation);
return [ cosZ, -sinA, 0,
sinA, cosZ, 0,
0, 0, 1 ];
}Um diese Matrizen multiplizieren zu können, wird die Funktion multiplyMatrix() gebraucht:
var multiplyMatrix = function(a, b) {
var newMatrix = [];
newMatrix[0] = a[0] * b[0] + a[1] * b[3] + a[2] * b[6];
newMatrix[1] = a[0] * b[1] + a[1] * b[4] + a[2] * b[7];
newMatrix[2] = a[0] * b[2] + a[1] * b[5] + a[2] * b[8];
newMatrix[3] = a[3] * b[0] + a[4] * b[3] + a[5] * b[6];
newMatrix[4] = a[3] * b[1] + a[4] * b[4] + a[5] * b[7];
newMatrix[5] = a[3] * b[2] + a[4] * b[5] + a[5] * b[8];
newMatrix[6] = a[6] * b[0] + a[7] * b[3] + a[8] * b[6];
newMatrix[7] = a[6] * b[1] + a[7] * b[4] + a[8] * b[7];
newMatrix[8] = a[6] * b[2] + a[7] * b[5] + a[8] * b[8];
return newMatrix;
}Damit schließlich die korrigierte Drehmatrix matrix auf den Normalenvektor normal angewenden werden kann, benötigen wir noch eine Funktion mulitplyVector(), welche beide miteinander multipliziert:
var multiplyVector = function(vector, matrix) {
var newVector = [];
newVector[0] = vector[0] * matrix[0] + vector[1] * matrix[1] + vector[2] * matrix[2];
newVector[1] = vector[0] * matrix[3] + vector[1] * matrix[4] + vector[2] * matrix[5];
newVector[2] = vector[0] * matrix[6] + vector[1] * matrix[7] + vector[2] * matrix[8];
return newVector;
}Am Ende dieser Berechnungen steht mit der Variable normal jederzeit der Normalenvektor des Geräts zur Verfügung, d.h. jener Vektor, der aus dem Bildschirm senkrecht heraus sticht. Seine Länge beträgt auch nach den Drehoperationen weiterhin 1.
Insofern das Endgerät korrekte gyroskopische Daten überträgt, haben wir nun einen Normalenvektor, der unabhängig von den browserspezifischen Intervallen immer in die richtige Richtung zeigt und die Ausrichtung des Geräts exakt beschreibt. Die einzelnen Koordinaten des Vektors können nun für weitere Berechnungen benutzt werden.
Einen Farbverlauf an der Geräteposition ausrichten
Zuerst brauchen wir eine einfache HTML-Struktur samt CSS.
<html lang="en">
<head>
<meta charset="utf-8">
<title>Gyroskop-Test</title>
<style>
html, body {
margin: 0;
padding: 0;
width: 100vw;
height: 100vh;
}
body {
font: 3vw/1.6 "Helvetica Neue", Helvetica, Arial, sans-serif;
background: #DDD;
color: #FFF;
}
.message {
position: absolute;
top: 50%;
left: 50%;
transform: translate(-50%, -50%);
width: 80%;
text-align: center;
}
</style>
</head>
<body>
<div class="message">Lade…</div>
</body>
</html>Die Funktion reactToPosition() ergänzen wir zum Schluss mit einem Aufruf der Funktion changeGradient():
var reactToPosition = function(orientation) {
var normal = false;
if (orientation !== false && orientation.alpha !== null &&
orientation.beta !== null && orientation.gamma !== null) {
normal = [0, 0, 1];
var matrix = getBaseRotationMatrix(orientation.alpha, orientation.beta, orientation.gamma);
matrix = multiplyMatrix(matrix, getScreenMatrix());
normal = multiplyVector(normal, matrix);
}
changeGradient(orientation, normal);
}changeGradient() soll nun sowohl den Farbverlauf für den body berechnen, als auch den Inhalt von div.message entsprechend anpassen.
var changeGradient = function(orientation, normal) {
var body = document.querySelector('body'),
el = document.querySelector('.message'),
msg, bg;
if (!normal) {
msg = "Dieses Gerät oder dieser Browser unterstützen keine Positionsdaten.";
bg = '#DDD';
} else {
…
}
el.innerHTML = msg;
body.style.background = bg;
}Da wir im Falle eines Fehlers in reactToPosition() für normal den Wert false übergeben, können wir in changeGradient() nun die entsprechende Meldung ausgeben und den Hintergrund grau darstellen.
Falls jedoch normal nicht als false evaluiert wird,Arrays konvertieren zu true, wenn sie als Boolean bestimmt werden. liegt ein Normalenvektor vor und kann in einen Farbverlauf entsprechend der CSS3-Syntax umgewandelt werden:
} else {
var deg = (1 - Math.abs(normal[2])) * orientation.alpha,
start = 50;
bg = 'linear-gradient(' + deg + 'deg, #C217F4 ' + start + '%, #141F93 ' + start + '%)';
msg = 'alpha: ' + orientation.alpha + 'beta: ' + orientation.beta + 'gamma: ' + orientation.gamma +
'Normal X: ' + normal[0] + 'Normal Y: ' + normal[1] + 'Normal Z: ' + normal[2] +
'Winkel: ' + deg + 'Start: ' + start;
}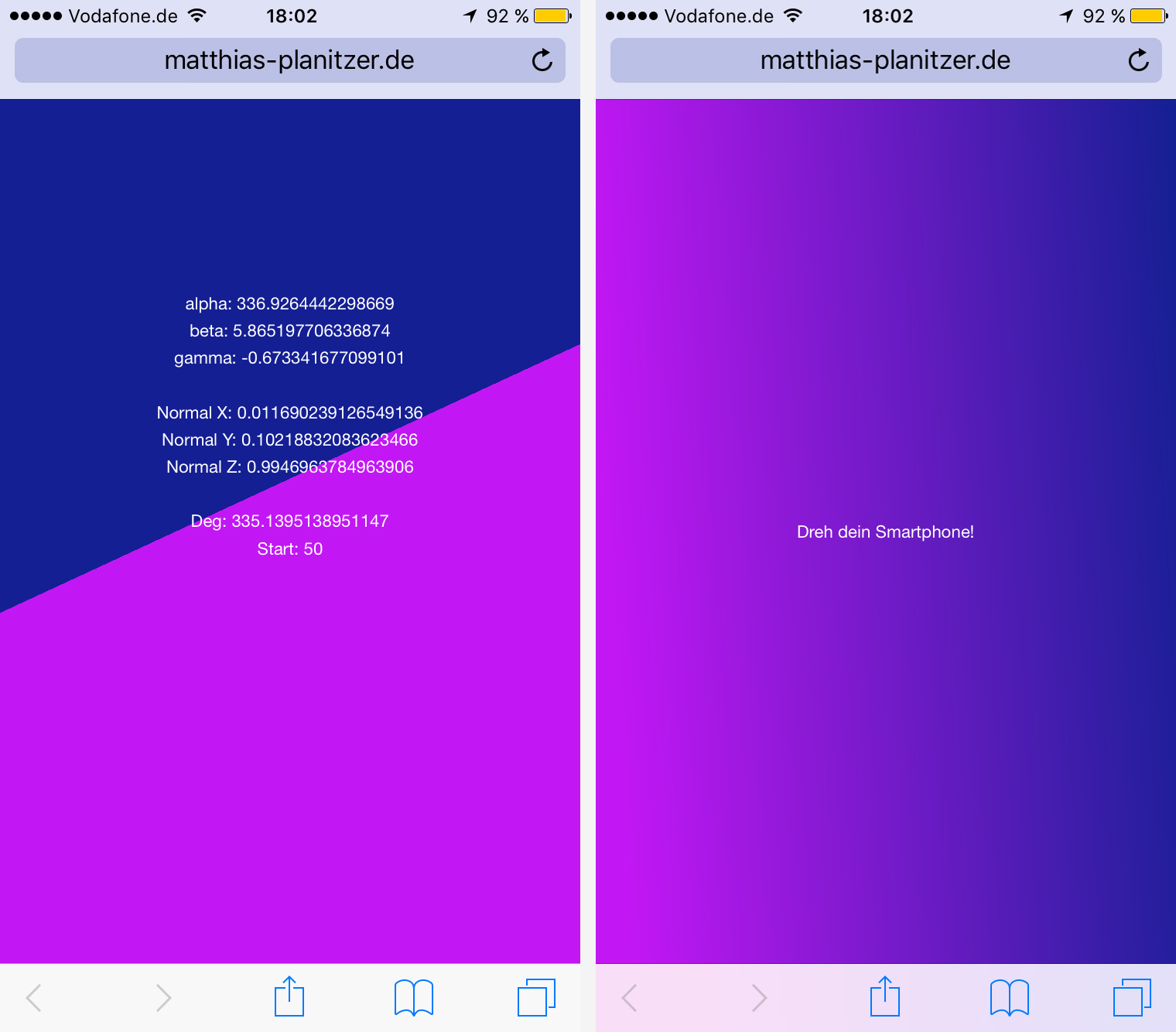
start = 50 sowie das Endergebnis.Trotz der längeren Berechnung des Normalenvektors benötigen wir weiterhin den alpha-Wert. Solange das Gerät flach gehalten wird, also die z-Koordinate des Normalenvektors nahezu 1 beträgt, gibt er die Drehung des Geräts in der horizontalen Ebene korrekt an. Mit zunehmender Schrägstellung, also Drehung um die x- oder y-Achse, unterliegt die Berechnung von alpha zunehmenden Störfaktoren, welche in Form eines plötzlichen Springens zwischen zwei entfernten Werten die Ausrichtung des Farbverlaufs ebenfalls springen lassen würden. Daher bringen wir normal[2] (die Länge des Normalenvektors entlang der z-Achse) wieder ins Spiel und bewirken, dass dieser Wert bei senkrecht stehendem Gerät gegen Null geht und somit den Winkel deg ebenfalls gegen Null gehen lässt.
Zu Testzwecken definieren wir zunächst sowohl den Start- als auch den Endwert des Verlaufs bei 50%, um einen harten Wechsel zwischen den beiden Farben zu erhalten und somit die Funktion des Scripts zu überprüfen. Anschließend können wir start so berechnen, dass die Variable ebenfalls von normal[2] abhängt.
var deg = (1 - Math.abs(normal[2])) * orientation.alpha,
start = 10 * Math.abs(normal[2]);
bg = 'linear-gradient(' + deg + 'deg, #C217F4 ' + start + '%, #141F93 100%)';
msg = 'Dreh dein Smartphone!';Damit ist der responsive Farbverlauf auch schon fertig. Probier die Live-Demo mit deinem Smartphone aus!
Eine Wasserwaage programmieren
Die Möglichkeiten, das Gyroskop einzusetzen, sind nahezu unbegrenzt. Von Kugellabyrinth-Spielen, über Kompasse bis hin zu komplexen VR- und AR-Anwendungen lässt sich einiges damit anstellen. Eine einfache Anwendung ist auch eine Wasserwaage. Dazu benutzen wir alle bisherigen Funktionen, verweisen aber in reactToPosition() auf die neue Funktion wasserWaage():
var reactToPosition = function(orientation) {
…
if (…) {
…
}
wasserWaage(orientation, normal);
}Und ergänzen die HTML-Struktur und das CSS entsprechend:
<body>
<div class="message">Lade…</div>
<div class="wasserwaage hidden">
<div class="bubble"></div>
<div class="markierung"></div>
</div>
</body>.message.showAngle {
width: 25vh;
z-index: 3;
font-size: 4vw;
color: #000;
}
.wasserwaage {
position: absolute;
top: 0;
left: calc(50vw - 15vh);
height: 100vh;
width: 30vh;
background-color: #32cd32;
}
.wasserwaage:before,
.wasserwaage:after {
content: '';
position: absolute;
top: 0;
width: 10px;
height: 100%;
z-index: 2;
}
.wasserwaage:before {
left: -10px;
background-image: linear-gradient(to left, #32cd32, transparent);
}
.wasserwaage:after {
right: -10px;
background-image: linear-gradient(to right, #32cd32, transparent);
}
.bubble {
position: absolute;
top: 50%;
left: 10px;
height: calc(30vh - 20px);
width: calc(100% - 20px);
transform: translateY(-50%);
border-radius: 30%;
background-color: white;
}
.markierung {
position: absolute;
top: calc(35% - 5px);
left: 0;
height: 30%;
width: 100%;
border-top: 5px solid #000;
border-bottom: 5px solid #000;
}
.hidden {
display: none;
}
@media screen and (max-width: 800px) and (orientation: landscape) {
.message.showAngle {
font-size: 2vw;
}
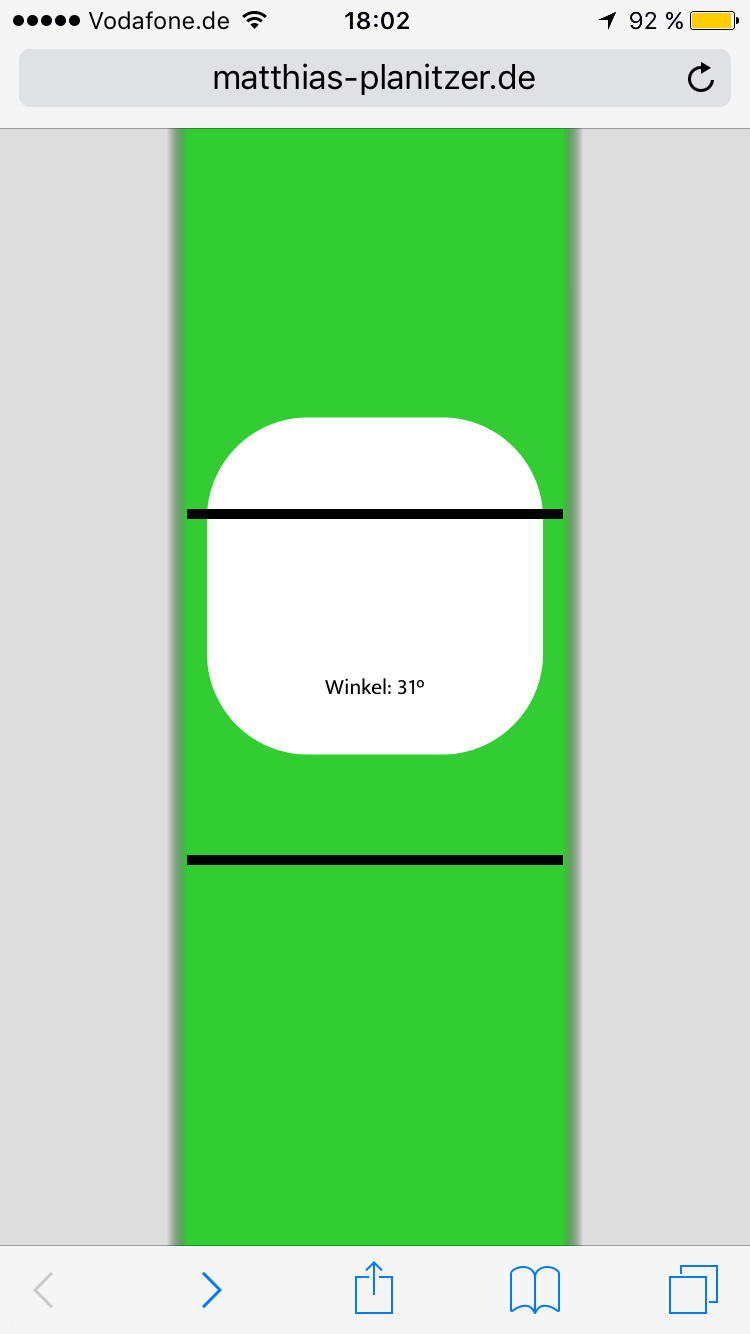
}In wasserWaage() lesen wir wieder je nach Ausrichtung des Geräts normal[2] oder normal[0] – also die Länge des Normalenvektors in Richtung der z- bzw. x-Achse und damit ein Maß der Neigung des Geräts zwischen Horizontale und Vertikale – aus und berechnen daraus zwei Größen: einerseits pos, den Abstand der Luftblase von der oberen Fensterkante, andererseits den Winkel deg, welcher sich zwischen dem Gerät und der Ebene entspannt. Dazu bemühen wir eine Funktion mapValue(), welche einen Wert aus einem Ausgangsintervall in ein Zielintervall überträgt.
var mapValue = function(value, minOrig, maxOrig, minResult, maxResult) {
return (value - minOrig) * (maxResult - minResult) / (maxOrig - minOrig) + minResult;
}
var wasserWaage = function(orientation, normal) {
var waage = document.querySelector('.wasserwaage'),
bubble = document.querySelector('.bubble'),
el = document.querySelector('.message'),
msg, pos, deg;
if (!normal) {
msg = 'Dieses Gerät oder dieser Browser unterstützen keine Positionsdaten.';
pos = 50;
el.classList.remove('showAngle');
waage.classList.add('hidden');
} else {
pos = (currentScreenOrientation == 0) ? normal[2] : normal[0];
deg = Math.floor(mapValue(pos, -1, 1, -180, 180));
pos = Math.floor(mapValue(pos, -1, 1, 100, 0));
msg = 'Winkel: ' + deg + '°';
el.classList.add('showAngle');
waage.classList.remove('hidden');
}
el.innerHTML = msg;
bubble.style.top = pos + '%';
}Mehr braucht es nicht für eine simple Wasserwaage. Probier die Live-Demo mit deinem Smartphone aus!